New HTB is finished. Finally. It's precision and speed amazed me when I tested it. I'm going to share the fun with you here. Of course there is still long way - we have to test it in real environment.
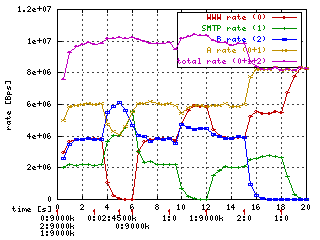
 Everyone who read my HTB manual knows the model situation I use. Three
leaves and two inner classes. Here you can see HTB3 performing at full
100Mbit rate on Pentium II/350. Blue line starts at 40Mbit which is bad.
It should be 60Mbit. It is because Ethloop simulator can't keep up at
these speeds. Unfortunately. But we can see that it
works - and it is most important after all.
Everyone who read my HTB manual knows the model situation I use. Three
leaves and two inner classes. Here you can see HTB3 performing at full
100Mbit rate on Pentium II/350. Blue line starts at 40Mbit which is bad.
It should be 60Mbit. It is because Ethloop simulator can't keep up at
these speeds. Unfortunately. But we can see that it
works - and it is most important after all.
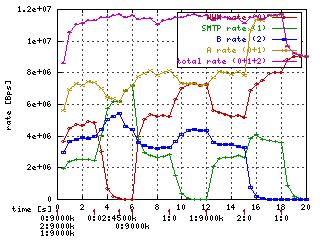
The second picture (at right) shows CBQ with the same (well almost) settings. I had to do some manual tweaking with maxburst and avgsize to make it work. You can see that there are errors in rates but at least it can do something at the same rate.
Quict test on loopback device showed me that it can do 0.5Gbit on my machine, however I have some problems with Ethloop at these rates.
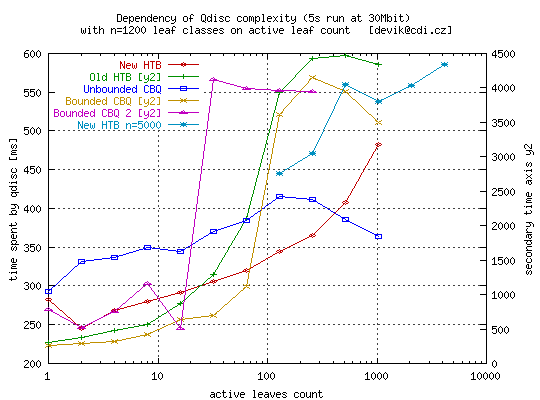
Each leaf has rate 8kbit while root has 30Mbit (except for n=5000 where I set root rate to 50Mbit). The script generated various Qdisc configuration (different lines in graph) and for each one it simulated flow with varying number of backlogged classes (I've written special test proggie for it). First let's look at old HTB (the one currently in common use). It is green line and you should use right scale (0 to 4.5sec). It is clearly O(N) complexity (here shown as exponential because of logarithmic x scale). Limiting at x=300 is due to lack of CPU resources for next growth.
Yellow line is very similar. It is CBQ with bounded root class. It was very hard
to tune all parameters to make it work with high number of leaves. The very first
attempt to set it up resulted into magenta line and totaly useless qdisc output
flow rates.
No surprise here. Old HTB uses almost the same approach as CBQ - even slower one.
Only question is: why CBQ complexity starts to decrease at x=400 ? It is becase
number of active classes is too close to total number of classes. Then probability
that we find leaf eligible to send without borrowing is increasing and we don't need
so much steps to find such leaf. Also top-level algorithm inside of CBQ shows
increasing preference of higher top-level values when all classes are backlogged
and dequeued often.
Blue line is unbounded CBQ. You can see that is is fastest one (we use left scale here !). Why so fast ? It is simple. The higher is number of active classes (and thus dequeue rate) the higher is probability that top-level variable will be in "infinity" state. In this state we can dequeue the first leaf we hit. This speedup acts against increasing linear complexity and resulting complexity is almost constant. However absolute error increases instead ...
Let's look at HTB3. You can see that it slowly increases in logarithmic scale so that we are between O(log N) and O(N). To clarify it further I extended the test to n=5000 (cyan line). Here we can see that increase in almost linear so that we are really close to O(log N). Also you can see that we are even faster than unbounded CBQ for less than 400 active classes (again we use left scale for both red and cyan line).
There are yet better Qdisc algos like H-FSC but these will be slower (arithmetic) and more complex. Also virtual clock algos are not the best bet for non work conserving Qdisc (shaper).
devik